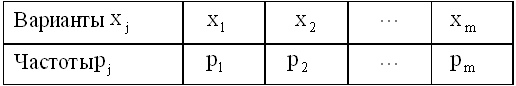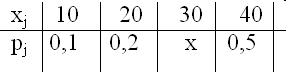Математическая статистика
- Дана выборка объема
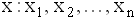 . Статистический (или эмпирический) начальный момент k-го порядка находится по формуле
. Статистический (или эмпирический) начальный момент k-го порядка находится по формуле
- Для 2-х нормальных независимых величин с одинаковыми дисперсиями получены выборки объема
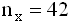 и
и 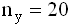 с такими характеристиками:
с такими характеристиками: 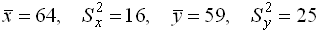 . При уровне значимости a=0.05 проверяется гипотеза о равенстве генеральных средних
. При уровне значимости a=0.05 проверяется гипотеза о равенстве генеральных средних 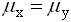 (конкурирующая гипотеза
(конкурирующая гипотеза 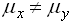 ). Область принятия гипотезы
). Область принятия гипотезы 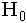 равна
равна
- Дана выборка объема
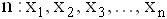 . Выборочное среднее находится по формуле
. Выборочное среднее находится по формуле
- По выборке объема n=9 вычислили выборочное среднее 15 и исправленную несмещенную дисперсию 9. 95%-ый доверительный интервал для математического ожидания m (t8,0.95=2,3) равен
- По выборке построена таблица статистического распределения выборки, имеющая вид.
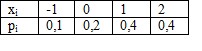
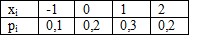
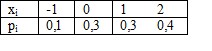
Дана выборка объема 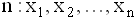 . Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее
. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее
- Известно, что X~N(0,3), Y~N(0.5, 2), Х и Y независимы. S=X+2Y имеет распределение
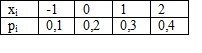
- Дано статистическое распределение выборки

Выборочное среднее 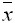 и выборочная дисперсия
и выборочная дисперсия 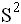 равны
равны
- Дано статистическое распределение выборки

График эмпирической функции распределения для этой выборки имеет вид
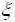 – стандартная нормальная случайная величина. Случайная величина
– стандартная нормальная случайная величина. Случайная величина 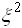 имеет распределение
имеет распределение- В итоге четырех измерений некоторой физической величины одним прибором получены следующие результаты: 8, 9, 11, 12. Выборочная средняя результатов измерений, выборочная и исправленная дисперсии ошибок прибора равны соответственно
- Случайная величина распределена равномерно на отрезке [0, 2]. Ее математическое ожидание равно
- Для упрощения счета из всех значений выборки вычли 1280. При этом эмпирическая дисперсия
- Дано статистическое распределение выборки

Выборочное среднее 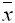 и выборочная дисперсия
и выборочная дисперсия 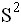 равны
равны
- Для построения доверительного интервала для дисперсии надо пользоваться таблицами
- Было проведено выборочное обследование доходов жителей. Оказалось, что половина жителей имеет доходы от 0 до 400 рублей, а половина – от 400 до 2000 рублей. По этим данным построили гистограмму. Она имеет вид
- Дано выборочное распределение

Значение полигона, построенного по данному выборочному распределению, в точке 1280 и моды равны
- Для того, чтобы по выборке объема n= 10 построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого неизвестна, нужны таблицы
- Случайная величина распределена «нормально с параметрами 3,2» (N[3,2]). Ее математическое ожидание и дисперсия равна
- Дана выборка объема
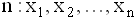 . Если каждый элемент выборки увеличить на 5 единиц, то
. Если каждый элемент выборки увеличить на 5 единиц, то
- Формула D(-X)=D(X)
- Случайная величина
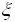 распределена равномерно на [0,1],
распределена равномерно на [0,1], 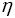 распределена равномерно на [2,6]. Ее можно получить из
распределена равномерно на [2,6]. Ее можно получить из 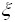 с помощью линейного преобразования
с помощью линейного преобразования
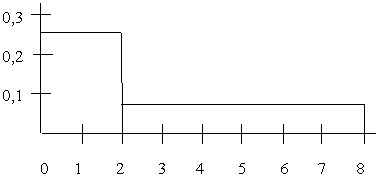
- Самое маленькое значение в выборке 0, самое большое 8, медиана 2. По этой выборке построена гистограмма
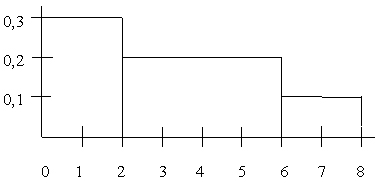
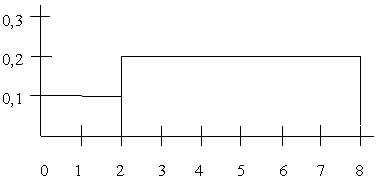
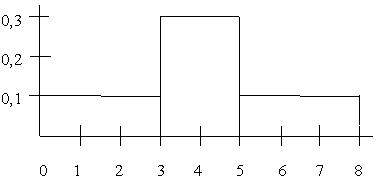
Распределение выборки рабочих по времени, затраченному на обработку одной детали, приведено в таблице

Эмпирическое среднее времени, затрачиваемого на обработку одной детали,
- Дана конкретная выборка объема n = 10: 2, 2, 5, 5, 4, 3, 4, 2, 2, 5. Статистическое распределение этой выборки имеет вид




Величина 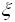 имеет распределение N(a,
имеет распределение N(a, 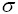 ). Вероятность p{
). Вероятность p{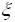 <a+2
<a+2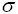 } равна
} равна
- Для обработки наблюдений методом наименьших квадратов построена прямая. Ее график:
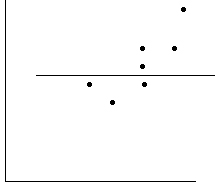
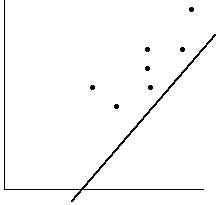
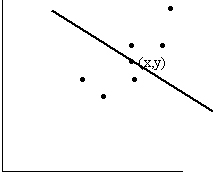
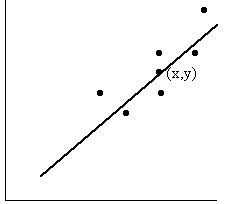
Для выборки объема n=9 рассчитали выборочную дисперсию 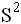 =3,86. Исправленная дисперсия равна
=3,86. Исправленная дисперсия равна
- Дано статистическое распределение выборки с числом вариант m:
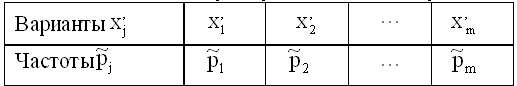
Статистический (или эмпирический) начальный момент k-го порядка находится по формуле
- По выборке построена гистограмма
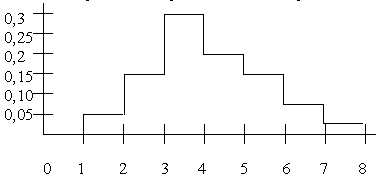
По виду гистограммы можно предполагать, что генеральная совокупность, из которой произведена выборка, имеет распределение
- Дана выборка объема n = 10: 2, 3, 5, 5, 6, 6, 7, 8, 9. Выборочное среднее равно
- Данные о прибыли, полученной в течение месяца, за последние 5 месяцев оказались следующими:

С помощью метода наименьших квадратов по этим точкам строится прямая регрессии. Эта прямая для прибыли в марте дает значение (Указание. Определить это значение без построения прямой регрессии)
- Из генеральной совокупности извлечена выборка, данные по ней сведены в таблицу

Оценка генеральной средней
- Дан вариационный ряд выборки объема n = 10: -2, 0, 3, 3, 4, 5, 9, 11, 12, 15. Выборочная медиана для этого ряда – d равна
- Для 2-х нормальных независимых величин с одинаковыми дисперсиями получены выборки объема
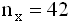 и
и 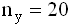 с такими характеристиками:
с такими характеристиками: 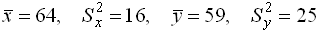 . При уровне значимости
. При уровне значимости 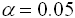 проверяется гипотеза о равенстве генеральных средних
проверяется гипотеза о равенстве генеральных средних 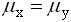 (конкурирующая гипотеза
(конкурирующая гипотеза 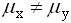 ). Область принятия гипотезы
). Область принятия гипотезы 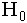 равна
равна
- Дано статистическое распределение выборки с числом вариант m:
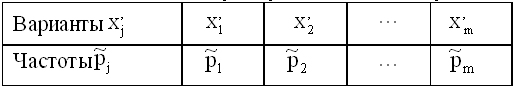
Выборочная средняя равна 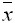 . Тогда статистический центральный момент k-го порядка находится по формуле:
. Тогда статистический центральный момент k-го порядка находится по формуле:
- По выборке построена гистограмма
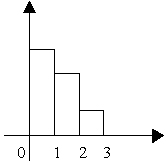
Медиана равна
- Вариационный ряд выборки: -7, 2, 4, 0, 3, 2, 1, -5 имеет вид
- Состоятельной, но смещенной точечной оценкой параметра является
- Математическое ожидание и дисперсия случайной величины, имеющей плотность распределения
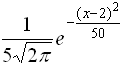 , равны
, равны
- Величина
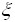 имеет распределение N(
имеет распределение N(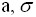 ). Вероятность
). Вероятность 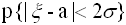 равна
равна
- Случайная величина X распределена «нормально с параметрами 3,2» - (N[3,2]). Для нее вероятность попасть внутрь интервала [-1,7] равна
- Медиана выборки

равна
- Для проверки гипотезы о равенстве 2-х генеральных средних надо пользоваться таблицами
- Дана выборка объема n = 5: -2, -1, 1, 3, 4. Выборочное среднее
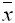 и выборочная дисперсия
и выборочная дисперсия 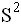 равны
равны
- Из генеральной совокупности извлечена выборка, данные по ней сведены в таблицу

Оценка генеральной средней
- Математическое ожидание и дисперсия случайной величины, распределенной равномерно на отрезке [1,3], равны
- Для упрощения счета из всех значений выборки вычли 1280. При этом эмпирическое среднее
- Дано статистическое распределение выборки с числом вариант m:
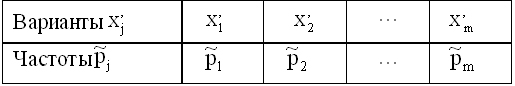
- Статистический (или эмпирический) начальный момент k-го порядка находится по формуле
- По выборке построена гистограмма
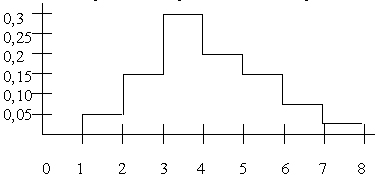
По виду гистограммы можно предполагать, что генеральная совокупность, из которой произведена выборка, имеет распределение
- Наблюдения проводились над системой (х, у) 2-х величин. Результаты наблюдения записаны в таблицу
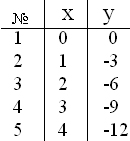
Коэффициент корреляции равен
- В таблице статистического распределения, построенного по выборке, одна цифра написана неразборчиво
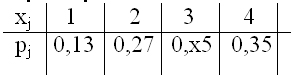
Эта цифра
- По выборке построена статистическая таблица распределения
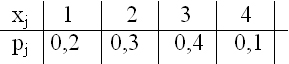
Значение выборочной медианы
- Наблюдения проводятся над системой (X : Y) двух случайных величин. Выборка состоит из пар чисел:
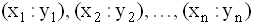 . Найдены
. Найдены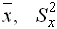 для
для 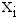 и
и 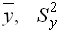 для
для 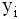 (
(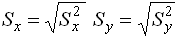 ). Тогда выборочный коэффициент корреляции
). Тогда выборочный коэффициент корреляции 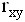 находится по формуле
находится по формуле
- Построить гистограмму и полигон распределения роста школьников по таблице
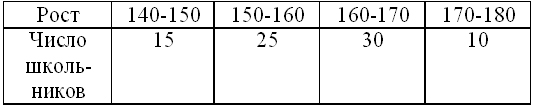
Построить графически моду, найти медиану
- Случайная величина X распределена «нормально с параметрами 0,1» - (N[0,1]). Для нее вероятность попасть внутрь интервала [-3,3] равна
- Дана выборка объема n = 7: 3, 5, -2, 1, 0, 4, 3. Вариационный ряд для этой выборки и размах вариационного ряда
- Случайная величина распределена равномерно на отрезке [0, 4]. Вероятность попасть в интервал [1,3] равна
- По выборке построен доверительный интервал для генерального среднего. Оказалась, что генеральное среднее по такому объему выборки определяется с точностью 0,2. Чтобы повысить точность вдвое, надо объем выборки
- Величина
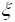 имеет распределение N(
имеет распределение N(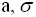 ). Вероятность
). Вероятность 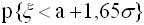 равна
равна
- Дана выборка объема n = 5: 2, 3, 5, 7, 8. Выборочное среднее
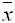 и выборочная дисперсия
и выборочная дисперсия 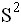 равны
равны
- Для того, чтобы вдвое сузить доверительный интервал, построенный для математического ожидания, во сколько раз надо увеличить число наблюдений
- Дано статистическое распределение выборки:

Выборочное среднее 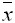 и выборочная дисперсия
и выборочная дисперсия 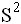 равны
равны
- Дано статистическое распределение выборки

Выборочное среднее 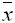 и выборочная дисперсия
и выборочная дисперсия 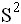 равны
равны
- Случайная величина X распределена «нормально с параметрами 3,2» - (N[3,2]). Случайная величина Y=(X-3)/2. Ее математическое ожидание, дисперсия и тип распределения
- Производится выборка объема n=100 из генеральной совокупности, имеющей распределение N (20,4). По выборке строится выборочное среднее
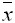 . Эта случайная величина имеет распределение
. Эта случайная величина имеет распределение
- Дан вариационный ряд выборки объема n = 9: -2, 0, 3, 3, 4, 5, 9, 11, 12. Выборочная медиана для этого ряда – d равна
- Дан вариационный ряд выборки объема n = 7: -5, -3, 0, 1, 1, 4, 16. Выборочная медиана d и выборочное среднее
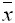 для этого ряда равны
для этого ряда равны
- По выборке построена таблица статистического распределения выборки. Эта таблица
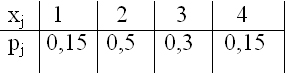
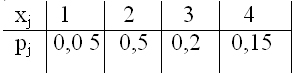
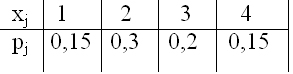
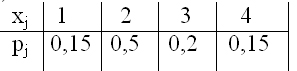
- По выборке объема n из нормального распределения с известной дисперсией
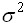 строится доверительный интервал для математического ожидания. Если объем выборки увеличить в 25 раз, длина доверительного интервала
строится доверительный интервал для математического ожидания. Если объем выборки увеличить в 25 раз, длина доверительного интервала
- Эмпирический коэффициент корреляции между весом и ростом для выборки

равен
- Дана выборка объема n = 10. Статистическое распределение этой выборки имеет вид

Тогда выборочное среднее для этой выборки равно
- Дана выборка объема n = 5: -6, -4, 0, 4, 6. Выборочное среднее
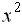 и выборочная дисперсия
и выборочная дисперсия 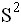 равны
равны
- Дана выборка объема
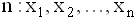 . Выборочная средняя равна
. Выборочная средняя равна 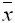 . Тогда статистический центральный момент k-го порядка находится по формуле
. Тогда статистический центральный момент k-го порядка находится по формуле
- Медиана выборки

равна
- Случайная величина X распределена равномерно на отрезке [0, 1]. Случайная величина Y=X+2 будет иметь
- По выборке объема n из нормального распределения с неизвестной дисперсией строится доверительный интервал для математического ожидания. Объем выборки увеличиваем в 16 раз. В предположении, что величины
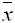 и
и 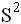 при этом изменятся мало, длина доверительного интервала примерно
при этом изменятся мало, длина доверительного интервала примерно
- Эмпирический коэффициент корреляции между весом и ростом для выборки

равен
- Для 2-х нормальных независимых величин с одинаковыми дисперсиями получены выборки объема
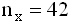 и
и 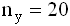 с такими характеристиками:
с такими характеристиками: 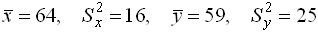 . При уровне значимости
. При уровне значимости 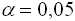 проверяется гипотеза о равенстве генеральных средних
проверяется гипотеза о равенстве генеральных средних 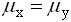 (конкурирующая гипотеза
(конкурирующая гипотеза 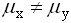 ). Опытное значение статистики Т, применяемой для проверки гипотезы
). Опытное значение статистики Т, применяемой для проверки гипотезы 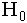 , равно 4,17. Гипотеза
, равно 4,17. Гипотеза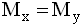
- Для сравнения 2-х генеральных средних совокупностей X и Y из них извлекли выборки объема n и m соответственно. Для проверки гипотезы о том, что
 , надо вычислить статистику
, надо вычислить статистику
- Значение кумуляты, построенной по таблице, в точке 170, и медианы равны

- Функцию распределения F(х) можно найти по плотности вероятности f(х) по формуле
- Дано статистическое распределение выборки с числом вариант m:
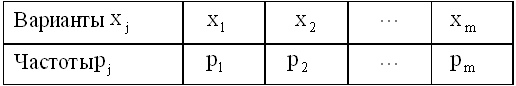
- Выборочная средняя равна
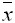 . Тогда выборочная дисперсия
. Тогда выборочная дисперсия 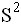 находится по формуле
находится по формуле
- Распределение выборки рабочих по времени, затраченному на обработку одной детали, приведено в таблице

Эмпирическое среднее времени, затрачиваемого на обработку одной детали,
- Плотность распределения f(x) можно найти по функции распределения F(х) по формуле
- По выборке объема 100 надо построить доверительный интервал для математического ожидания нормального распределения, дисперсия которого известна. Для этого необходимо воспользоваться
- Дан вариационный ряд выборки объема n = 8: -2, 0, 3, 4, 6, 9, 12, 16. Выборочная медиана d и выборочное среднее
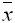 для этого ряда равны
для этого ряда равны
- Дана выборка объема n = 10. Статистическое распределение этой выборки имеет вид

- Тогда выборочное среднее
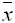 для этой выборки равно
для этой выборки равно
- Всегда ли верна формула M(X+Y)=M(X)+M(Y)
- Наблюдения проводились над системой (х, у) 2-х величин. Результаты наблюдения записаны в таблицу
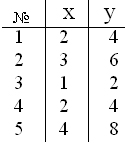
Коэффициент корреляции равен
- В таблице статистического распределения, построенного по выборке, на одно число попала клякса
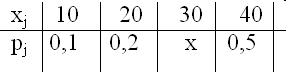
Это число
- По выборке объема n=100 вычислены выборочное среднее – 54 и выборочная дисперсия – 16. 95%-ый доверительный интервал для генерального среднего равен




![]() . Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее
. Если каждый элемент выборки увеличить в 5 раз, то выборочное среднее
![]() и выборочная дисперсия
и выборочная дисперсия ![]() равны
равны

![]() и выборочная дисперсия
и выборочная дисперсия ![]() равны
равны









![]() имеет распределение N(a,
имеет распределение N(a, ![]() ). Вероятность p{
). Вероятность p{![]() <a+2
<a+2![]() } равна
} равна



![]() =3,86. Исправленная дисперсия равна
=3,86. Исправленная дисперсия равна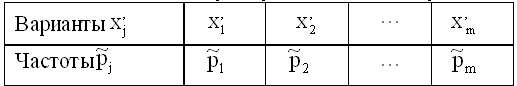

![]()
![]()
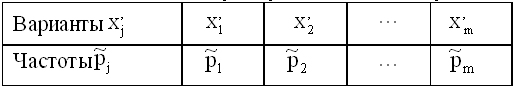
![]() . Тогда статистический центральный момент k-го порядка находится по формуле:
. Тогда статистический центральный момент k-го порядка находится по формуле:
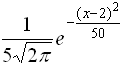 , равны
, равны
![]()
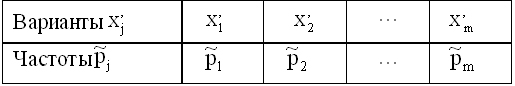


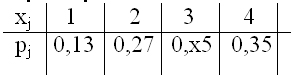
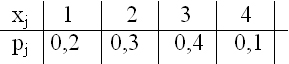


![]() и выборочная дисперсия
и выборочная дисперсия ![]() равны
равны
![]() и выборочная дисперсия
и выборочная дисперсия ![]() равны
равны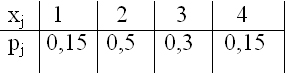
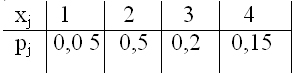
![]()

![]()
![]()